Tree Traversal or Traversing a binary tree is a method that refers as "to visit each node of tree in a specified order(exactly one tim...
Tree Traversal or Traversing a binary tree is a method that refers as "to visit each node of tree in a specified order(exactly one times per node)".
Ways to traverse the tree:-
1)In-order Traversal:-
Procedure:-1)Traverse the left sub-tree.
2)Visits Root node.
3)Post Order traversal.
In simple words....Left-->Root-->Right or L(e)-->R-->R(i)
2)Post Order Traversal:-
Procedure:-1)Traverse Right Sub Tree.
2)Traverse Left Sub Tree.
3)Visits Root node.
In simple words....Right-->Left-->Root R(i)-->L(e)-->R
3)Preorder Traversal:-
Procedure:-1)Visits Root node.
2)Traverse Left Sub Tree.
3)Traverse Right Sub Tree.
In simple words....Root-->Left-->Right or R-->L(e)-->R(i)
Let us take an examples:-
Example 1:-
In Order:-E,B,D,G,K,J,I,H,F,A,C,N,M.
Post order:-E,K,J,I,H,G,F,D,B,N,M,C,A.
Preorder:-A,B,E,D,F,G,H,I,J,K,C,M,N.
Example 2:-
In Order:-K,G,L,H,M,D,B,A,E,O,Q,R,S,T,P,N,C.
Post Order:-K,L,M,H,G,D,B,T,S,R,Q,P,O,N,E,C,A.
Preorder:-A,B,D,G,K,L,H,M,C,E,N,O,P,Q,R,S,T.
Example 3:-(a*b)+(c/d)-e+(f^g)
In order:-a*b+c/d-e+f^g.
Post Order:-ab*cd/+efg^+-.
Preorder:--+*ab/cd+e^fg.
Example:- 4:-a*(b+c)-d/e+(f%g)^h.
In Order:-a*b+c-d/e+f%g^h.
Post Order:-abc+*de/-fg%h^+.
Preorder:-+-*a+bc/de^%fgh.
Ways to traverse the tree:-
1)In-order Traversal:-
Procedure:-1)Traverse the left sub-tree.
2)Visits Root node.
3)Post Order traversal.
In simple words....Left-->Root-->Right or L(e)-->R-->R(i)
2)Post Order Traversal:-
Procedure:-1)Traverse Right Sub Tree.
2)Traverse Left Sub Tree.
3)Visits Root node.
In simple words....Right-->Left-->Root R(i)-->L(e)-->R
3)Preorder Traversal:-
Procedure:-1)Visits Root node.
2)Traverse Left Sub Tree.
3)Traverse Right Sub Tree.
In simple words....Root-->Left-->Right or R-->L(e)-->R(i)
Let us take an examples:-
Example 1:-
In Order:-E,B,D,G,K,J,I,H,F,A,C,N,M.
Post order:-E,K,J,I,H,G,F,D,B,N,M,C,A.
Preorder:-A,B,E,D,F,G,H,I,J,K,C,M,N.
Example 2:-
In Order:-K,G,L,H,M,D,B,A,E,O,Q,R,S,T,P,N,C.
Post Order:-K,L,M,H,G,D,B,T,S,R,Q,P,O,N,E,C,A.
Preorder:-A,B,D,G,K,L,H,M,C,E,N,O,P,Q,R,S,T.
Example 3:-(a*b)+(c/d)-e+(f^g)
In order:-a*b+c/d-e+f^g.
Post Order:-ab*cd/+efg^+-.
Preorder:--+*ab/cd+e^fg.
Example:- 4:-a*(b+c)-d/e+(f%g)^h.
In Order:-a*b+c-d/e+f%g^h.
Post Order:-abc+*de/-fg%h^+.
Preorder:-+-*a+bc/de^%fgh.
If you have any query then leave your comments and don't forgot to follow me on Google+,Facebook,Twitter.



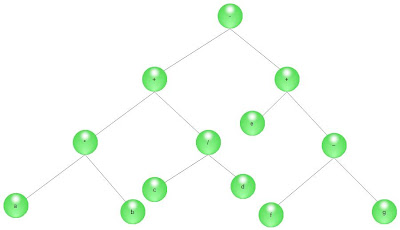







according to example 1, the Post order should be:-E,K,J,I,H,G,F,D,B,N,M,C,A.
ReplyDeleteyeah..due to some error I made it wrong but thanks for correction.
ReplyDeleteSo in place B its D and in place of D its B......but now its corrected.
ReplyDelete